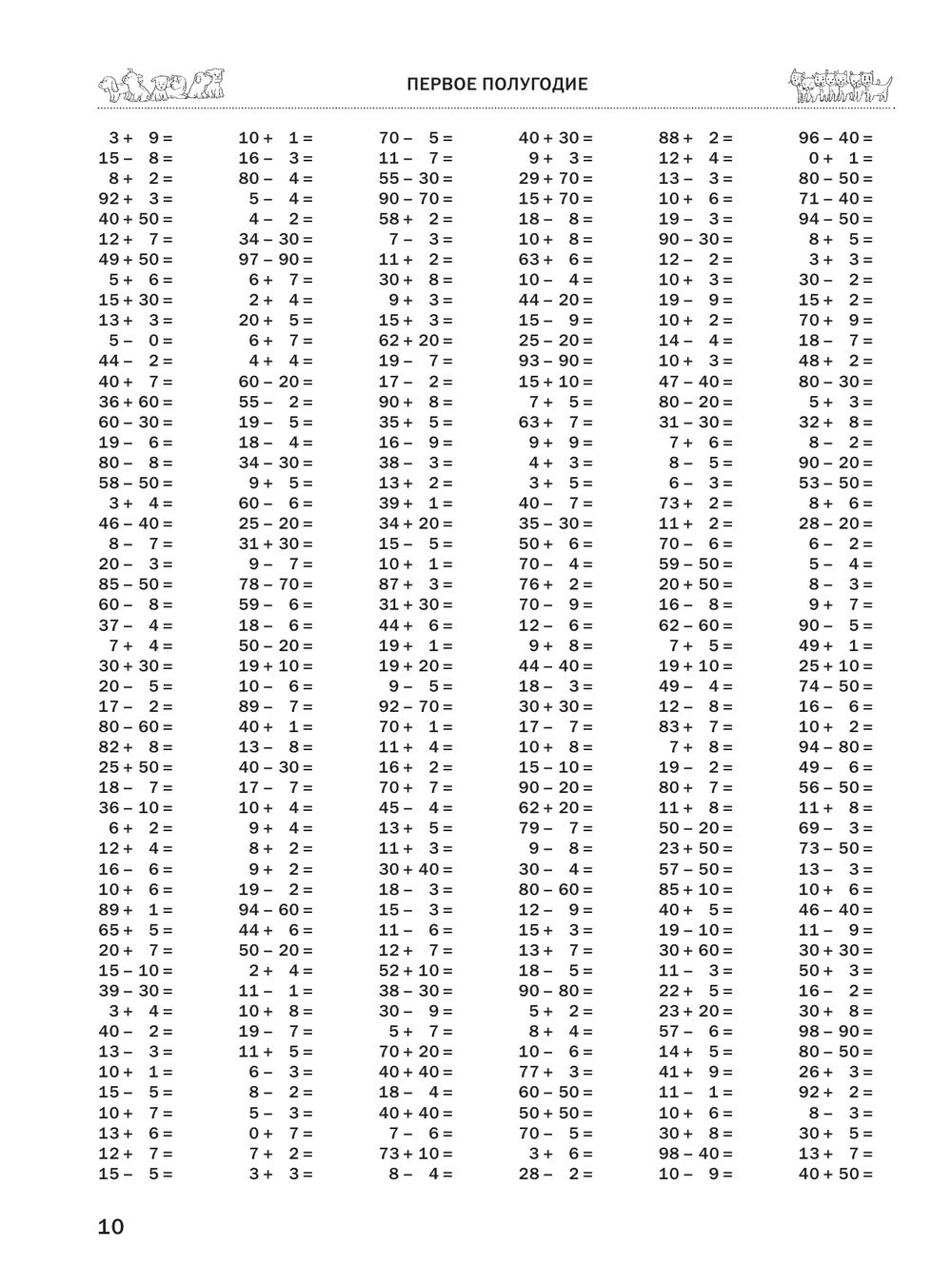
Устный Счет По Таблице Умножения
- Устный Счет Таблица Умножения Презентация
- Устный Счет Таблица Умножения 2 Класс
- Устный Счет Таблица Умножения И Деления
- Устный Счет Таблица Умножения 3 Класс Карточки
- Устный Счет Таблица Умножения 3 Класс
Муниципальное общеобразовательное учреждение средняя общеобразовательная школа №2 муниципального образования город Горячий Ключ Урок по теме: Комбинаторика. Комбинаторные задачи. Учитель математики Минасян Людмила Григорьевна МБОУ СОШ №2 г.Горячий Ключ Цель урока: познакомить учащихся с разделом математики – комбинаторикой.
Показать решение некоторых комбинаторных задач. Ход урока: а) объяснение материала; б) закрепление материала, решение задач.
Презентация для школьников на тему '«Табличное умножение и деление» Устный счёт' по математике. PptCloud.ru — удобный каталог с возможностью скачать powerpoint презентацию бесплатно. Pptx (powerpoint). У резной избушкиНа лесной опушкеБельчата гуляли,Орехи считали.На 6 кучек разделили,В каждую кучку по 3 положили.Если таблицу умножения знаешь,То без труда орехи сосчитаешь. На пригорке возле ёлок Ёжик яблоки считал: Семь под ёлкой, семь за ёлкой, Семь в мешке за тем пригорком, Семь в избе на третьей полке, Семь под лавкою в саду. Тренажёры по таблице умножения и деления (Excel). Можно потренировать устный счет.
В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитать число комбинаций. Такие задачи называются комбинаторными задачами, а раздел математики, в котором рассматриваются эти задачи, называется комбинаторикой. Слово «комбинаторика» происходит от латинского слова combinate, которое означает «соединять», «сочетать». Рассмотрим такой пример1. На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс, а запить их он может кофе, соком или кефиром.
Из скольких вариантов завтрака Вова может выбирать? Плюшка Бутерброд Пряник Кекс Кофе Кофе Плюшка Кофе Бутерброд Кофе Пряник Кофе Кекс Сок Сок Плюшка Сок Бутерброд Сок Пряник Сок Кекс Кефир Кефир Плюшка Кефир Бутерброд Кефир Пряник Кефир Кекс Всего вариантов столько же, сколько клеток в таблице. Однако составлять такие таблицы для каждой задачи, занимает время. Весняк нежность ноты.
Устный Счет Таблица Умножения Презентация
А чтобы решить такую задачу быстрее, можно воспользоваться правилом умножения. Правило умножения. Для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.

Устный Счет Таблица Умножения 2 Класс
Несколько стран в качестве символа своего государства решили использовать флаг в виде трех горизонтальных полос одинаковых по ширине, но разных по цвету: белый, синий, красный. Сколько стран могут использовать такую символику при условии, что у каждой страны свой, отличный от других, флаг? Решение будем искать с помощью «дерева возможных вариантов». Посмотрим на левую «веточку», идущую от «флага», пусть верхняя полоса – белого цвета, тогда средняя полоса может быть синей или красной, а нижняя – соответственно, красной или синей. Получилось два варианта цветов полос флага: белая, синяя, красная и белая, красная, синяя. Пусть теперь верхняя полоса – синего цвета, это вторая «веточка». Тогда средняя полоса может быть белой или красной, а нижняя - соответственно, красной или белой.
Получилось еще два варианта цветов полос: синяя, белая, красная и синяя, красная, белая. Аналогично рассматривается случай для верхней полосы красного цвета.
Устный Счет Таблица Умножения И Деления
Получается еще два варианта: красная, белая, синяя и красная, синяя, белая. Всего 6 комбинаций.
Построенная схема действительно напоминает дерево, только перевернутое. Поэтому ее называют «деревом возможных вариантов». А вот так выглядит «дерево возможных вариантов» для такого примера 3: Пример 3. Сколько трехзначных чисел можно составить из цифр 1, 3, 5 и 7, используя в записи числа каждую из них не более одного раза? Однако многие задачи можно решить быстрее и легче. Для этого надо знать простейшие комбинации, которые можно составлять из элементов конечного множества.
И одна из первых таких комбинаций - перестановки. Рассмотрим пример. Имеются три книги. Обозначим их буквами a,b и c.Эти книги нужно расставить на полке по-разному: а b с, а с b, b а с, b с а, с а b, с b. Каждое из этих расположений и называют перестановкой из трех элементов.
Перестановкой из n элементов называют каждое расположение этих элементов в определенном порядке. Обозначают: Рn = n! (n факториал). А теперь рассмотрим такой сюжет: Имеется 5 гвоздик разного цвета. Обозначим их буквами a, b, c, d, e. Требуется составить букет из трех гвоздик. Выясним, какие букеты можно составить.
Официальный руссификатор World Of Warcraft BC 2.4.3. Установка: 1. Убеждаемся, что у вас стоит версия клиента 2.4.3 (в противном случае качаем. Русификатор wow bc 2.4 3.
Вы не можете жить без интересных игры и приложения для мобильных телефонов? Wi-Money Manager ( Учет финансов Менеджер покупок ) Версия написания: jar Описание: Wi-Money Manager - это программа для учета персональных финансов, составления списков покупок, с возможностью синхронизации нескольких устройств. Вам каждый день хочется скачать новые игры на мобильный телефон? Вы хотите купить новый или и хотите знать на что ВАШ мобильный телефон способен? Скайп для самсунг gt-s5260. TOP 20 всех игр • 1) • 2) • 3) • 4) • 5) • 6) • 7) • 8) • 9) • 10) • 11) • 12) • 13) • 14) • 15) • 16) • 17) • 18) • 19) • 20) TOP 20 всех программ • 1) • 2) • 3) • 4) • 5) • 6) • 7) • 8) • 9) • 10) • 11) • 12) • 13) • 14) • 15) • 16) • 17) • 18) • 19) • 20) Друзья сайта:||||||||.
Если в букет входит гвоздика a, то можно составить такие букеты: abc, abd, abc, acd, ace, adc. Если в букет не входит гвоздика a, а входит гвоздика b, то можно получить такие букеты: bcd, bce, bdc. Наконец, если в букет не входит ни гвоздика a,гвоздика b, то можно составить букет cde. Мы показали все возможные способы составления букетов, в которых по-разному сочетаются три гвоздики из данных пяти.
Говорят, что составлены всевозможные сочетания из 5-ти элементов по 3. Сочетанием из n элементов по k называется любое множество, составленное из k элементов, выбранных из данных n элементов и обозначается С. Муниципальное общеобразовательное учреждение средняя общеобразовательная школа №2 муниципального образования город Горячий Ключ Урок по теме: Комбинаторика. Комбинаторные задачи. Учитель математики Минасян Людмила Григорьевна МБОУ СОШ №2 г.Горячий Ключ Цель урока: познакомить учащихся с разделом математики – комбинаторикой.
Показать решение некоторых комбинаторных задач. Ход урока: а) объяснение материала; б) закрепление материала, решение задач. В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитать число комбинаций. Такие задачи называются комбинаторными задачами, а раздел математики, в котором рассматриваются эти задачи, называется комбинаторикой. Слово «комбинаторика» происходит от латинского слова combinate, которое означает «соединять», «сочетать». Рассмотрим такой пример1.
На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс, а запить их он может кофе, соком или кефиром. Из скольких вариантов завтрака Вова может выбирать? Плюшка Бутерброд Пряник Кекс Кофе Кофе Плюшка Кофе Бутерброд Кофе Пряник Кофе Кекс Сок Сок Плюшка Сок Бутерброд Сок Пряник Сок Кекс Кефир Кефир Плюшка Кефир Бутерброд Кефир Пряник Кефир Кекс Всего вариантов столько же, сколько клеток в таблице. Однако составлять такие таблицы для каждой задачи, занимает время. А чтобы решить такую задачу быстрее, можно воспользоваться правилом умножения.
Правило умножения. Для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.
Устный Счет Таблица Умножения 3 Класс Карточки
Несколько стран в качестве символа своего государства решили использовать флаг в виде трех горизонтальных полос одинаковых по ширине, но разных по цвету: белый, синий, красный. Сколько стран могут использовать такую символику при условии, что у каждой страны свой, отличный от других, флаг? Решение будем искать с помощью «дерева возможных вариантов». Посмотрим на левую «веточку», идущую от «флага», пусть верхняя полоса – белого цвета, тогда средняя полоса может быть синей или красной, а нижняя – соответственно, красной или синей. Получилось два варианта цветов полос флага: белая, синяя, красная и белая, красная, синяя. Пусть теперь верхняя полоса – синего цвета, это вторая «веточка».
Тогда средняя полоса может быть белой или красной, а нижняя - соответственно, красной или белой. Получилось еще два варианта цветов полос: синяя, белая, красная и синяя, красная, белая. Аналогично рассматривается случай для верхней полосы красного цвета. Получается еще два варианта: красная, белая, синяя и красная, синяя, белая. Всего 6 комбинаций.
Построенная схема действительно напоминает дерево, только перевернутое. Поэтому ее называют «деревом возможных вариантов». А вот так выглядит «дерево возможных вариантов» для такого примера 3: Пример 3.
Сколько трехзначных чисел можно составить из цифр 1, 3, 5 и 7, используя в записи числа каждую из них не более одного раза? Однако многие задачи можно решить быстрее и легче. Для этого надо знать простейшие комбинации, которые можно составлять из элементов конечного множества. И одна из первых таких комбинаций - перестановки.
Устный Счет Таблица Умножения 3 Класс
Рассмотрим пример. Имеются три книги. Обозначим их буквами a,b и c.Эти книги нужно расставить на полке по-разному: а b с, а с b, b а с, b с а, с а b, с b. Каждое из этих расположений и называют перестановкой из трех элементов. Перестановкой из n элементов называют каждое расположение этих элементов в определенном порядке. Обозначают: Рn = n! (n факториал).
А теперь рассмотрим такой сюжет: Имеется 5 гвоздик разного цвета. Обозначим их буквами a, b, c, d, e. Требуется составить букет из трех гвоздик. Выясним, какие букеты можно составить. Если в букет входит гвоздика a, то можно составить такие букеты: abc, abd, abc, acd, ace, adc. Если в букет не входит гвоздика a, а входит гвоздика b, то можно получить такие букеты: bcd, bce, bdc.
Наконец, если в букет не входит ни гвоздика a,гвоздика b, то можно составить букет cde. Мы показали все возможные способы составления букетов, в которых по-разному сочетаются три гвоздики из данных пяти. Говорят, что составлены всевозможные сочетания из 5-ти элементов по 3. Сочетанием из n элементов по k называется любое множество, составленное из k элементов, выбранных из данных n элементов и обозначается С.